Difference between revisions of "Seismic Fragility Calculations (Task 10)"
SeismicAdmin (talk | contribs) |
SeismicAdmin (talk | contribs) m (1 revision imported) |
(No difference)
| |
Revision as of 17:15, 31 May 2022
Task Overview
Objective
This task is to estimate the conditional probabilities of structural or equipment failures for a given level of seismic ground motion for the screened-in components.
Purpose
The objective of a fragility evaluation is to estimate the capacity of a given component in terms of a ground motion parameter such as PGA or spectral acceleration. Typically, the seismic hazard for a plant site is defined by PGA or spectral accelerations (Sa) at different structural frequencies. Spectral acceleration is considered a good indicator of structural damage and is sometimes preferred as the ground motion parameter for fragility analysis. However, most existing hazard studies have focused primarily on PGA; therefore, most SPRAs have been based on PGA.
Guidance
Seismic Fragility Concepts
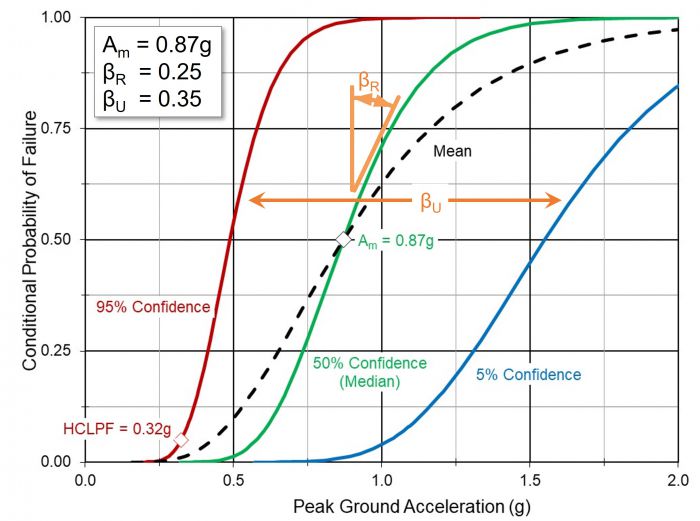
Seismic fragility is typically modeled by a lognormal cumulative probability distribution. The fragility calculation uses a double lognormal model with three parameters:
- Median acceleration capacity (Am),
- Logarithmic standard deviation of the aleatory (randomness) uncertainty in capacity (βR), and
- Logarithmic standard deviation of the epistemic (modeling and data) uncertainty in the median capacity (βU).
The aleatory and epistemic uncertainty can be combined using a square root of sum of squares (SRSS) method into a composite variability (βC), producing a mean fragility curve. Another key point is the high confidence of a low probability of failure (HCLPF), which is the 95% confidence of a less than 5% probability of failure. The figure below depicts these elements of the fragility curve using an example Am of 0.87g, βR of 0.25, and βU of 0.35. The fragility is defined by the following equation.
- a = Am * e(zβR) * e(zβU)
where:
- Am is the median capacity
- βR is the logarithmic standard deviation of the aleatory uncertainty
- βU is the logarithmic standard deviation of the epistemic uncertainty
- z is the standard normal variable corresponding to a defined non-exceedance probability
At a 95% confidence level (e(-1.65βU)) and a 5% probability of failure (e(-1.65βR)), the HCLPF is:
- HCLPF = Am * e[-1.65*(βR + βU)]
The example fragility curve below shows that the conditional probability of failure of a component increases with the ground motion level and approaches 1.0 at high accelerations. At relatively low ground motion values the conditional probability of failure is small but not zero. Even at ground motions less than the design basis acceleration, there will be some low probability of failure.
An SSC fragility is essentially calculated as the ratio of the SSC seismic capacity to the SSC seismic demand at its mounting point. The seismic capacity of an SSC is essentially fixed, although the demand varies with the location in the plant. For example the seismic capacity of a pump would be the same no matter where it is located in the plant but the seismic demand would typically be lower in the basement and higher as you go up in the building. In this scenario, the probability of failure would increase for pumps located higher in the building. This would be reflected as a lower median capacity, Am.
A given SSC may have different potential failure modes, each with their own fragility. A pump may have failure modes associated with providing pressure integrity, or positive flow, or anchorage. The fragility analyst may not explicitly calculate each of those fragilities, but it is important for the analyst to coordinate with the SPRA systems analyst to ensure the govern fragility is associated with the SSC function(s) credited in the systems model.
Seismic Fragility Calculation Methods
The most common methods for calculating seismic fragilities are the conservative deterministic failure margin (CDFM) method, also known as the hybrid method, and the separation of variables (SOV) method. Because only a handful of components are risk-significant enough to justify the additional effort required by the SOV approach, the hybrid method can provide efficiencies in the overall effort. The risk-significance of an SSC can be determined based on the Seismic PRA quantification output results discussed in Task 14. If an SSC is identified to be risk-significant (e.g., Fussell-Vesely greater than 5E-3), then the seismic fragility may be recalculated using the SOV method.
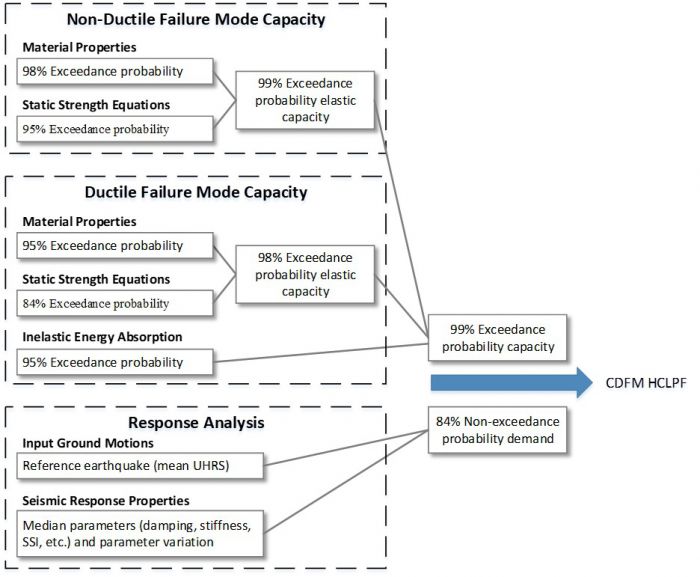
The hybrid fragility approach is a simplified method for estimating fragility curves, using the CDFM method to establish a HCLPF capacity, and a composite logarithmic standard deviation βC estimate is used estimate the mean fragility curve. Generic estimates of βR and βU can be used to develop the complete suite of SSC fragility curves. In the CDFM method defined levels of conservatism are used in the physical properties and analysis methods to calculate seismic capacity and demand. The levels of conservatism are similar or identical to those incorporated in typical structural design methods, which makes the CDFM method a more familiar approach that can be consistently performed by most engineers familiar with design evaluation methods. The figure below provides a general outline of the inputs to the CDFM method used to achieve a 99% exceedance probability capacity and an 84% non-exceedance probability seismic demand.
Due to the double lognormal nature of fragility curves, the HCLPF value (95% confidence of a less than 5% probability of failure) is approximately equal to the 1% probability of failure capacity on the mean fragility curve. Therefore, the mean fragility curve is estimated using the HCLPF value and an estimated composite βC.
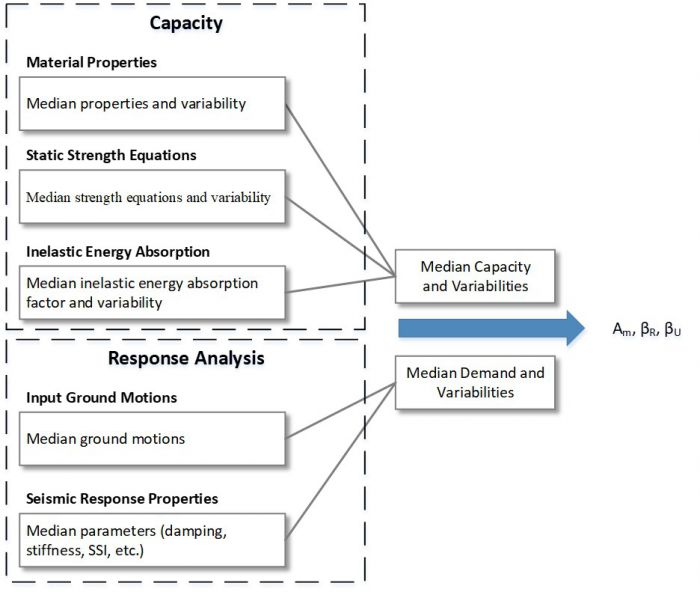
The SOV method explicitly characterizes a probability distribution (median value, aleatory variability, and epistemic variability) for each parameter affecting the SSC’s response and capacity. The final fragility distribution is obtained from the individual variables using the mathematical properties of lognormal distributions. The SOV method is typically the preferred method for SSCs that are dominant risk contributors or are risk significant in the seismic accident sequences. The figure below provides a general outline of the inputs used to achieve median estimates of the seismic capacity, seismic demand, and associated aleatory variabilities, and epistemic variabilities.
Supplemental Guidance
Related Element of ASME/PRA Standard
Part 5, Seismic Fragility-Response (SFR)
EPRI Guidance
Seismic Fragility and Seismic Margin Guidance for Seismic Probabilistic Risk Assessments (3002012994)
A Methodology for Assessment of Nuclear Plant Seismic Margin (NP-6041-SLR1)
Seismic Fragility Strength Equation Recommendations for Embedded Anchors (3002008099)
Review and Compilation of SQURTS Test Data for Use in Seismic Fragility Evaluations (3002010668)
Seismic Fragility Guidance for Pressurized Water Reactor Nuclear Steam Supply System Components (3002015988)
Loss of Offsite Power Seismic Fragility Guidance (3002015993)
Updated Equipment Seismic Capacities from Experience Data for Use in Fragility Calculations (3002011627)
Updated Equipment Seismic Capacities from Experience Data for Use in Fragility Calculations: Phase II (3002013017)
Guidance for Out-Of-Plane Shear Capacity of Reinforced Concrete Walls for Use in Fragility and Margin Calculations (3002018218)
Other Guidance
NUREG/CR-2300, "PRA Procedures Guide, A Guide to the Performance of Probabilistic Risk Assessments for Nuclear Power Plants" (Vol 1 and 2)